Ich habe Schema S mit den Attributen A, B, C, D, E, F und G.
Ich habe ausserdem einige funktionale Abhängigkeiten:
Punkt 2: Aber ich habe nicht verstanden, wie ich herausfinden kann, dass nur B und G complete und minimal sind. Ich habe zwar verstanden, was complete und minimal bedeutet, kann es aber bei diesem BSP nicht anwenden.
In der Musterlösung steht als Zwischenschritt zwischen Punkt 1 und Punkt 2:
AC(B)=S
AC(G)=S
AC(A)=S
Das ist wohl der Baustein, der mir fehlt. Aber ich kann es weder lesen (->Bedeutung der Klammer) noch verstehen.
Es folgt Aufgabe und Musterlösung. Ich habe keine Rechte zu diesen Dokumenten. Bitte löschen falls nötig.
Aufgabe:
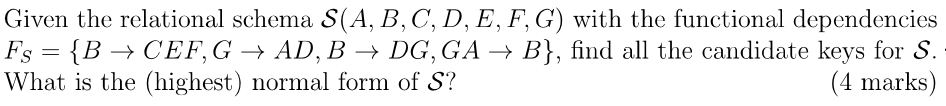
Musterlösung:

Vielen Dank für Eure Hilfe!
SQuaehLer
Ich habe ausserdem einige funktionale Abhängigkeiten:
- B -> CEF
- G -> AD
- B -> DG
- GA -> B
Punkt 2: Aber ich habe nicht verstanden, wie ich herausfinden kann, dass nur B und G complete und minimal sind. Ich habe zwar verstanden, was complete und minimal bedeutet, kann es aber bei diesem BSP nicht anwenden.
In der Musterlösung steht als Zwischenschritt zwischen Punkt 1 und Punkt 2:
AC(B)=S
AC(G)=S
AC(A)=S
Das ist wohl der Baustein, der mir fehlt. Aber ich kann es weder lesen (->Bedeutung der Klammer) noch verstehen.
Es folgt Aufgabe und Musterlösung. Ich habe keine Rechte zu diesen Dokumenten. Bitte löschen falls nötig.
Aufgabe:
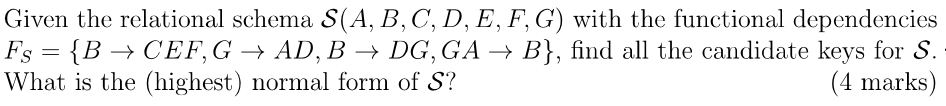
Musterlösung:

Vielen Dank für Eure Hilfe!
SQuaehLer
