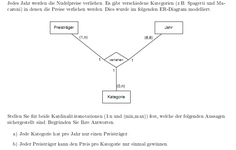
hallo, hab folgendes problem: Und zwar versteh die min-max - notation nicht ganz. Diese Aufgabe(s. bild) hab ich im inet gefunden und versucht zu lösen. bin aber nicht weit gekommen.
bei der Kardinalitätsrelation 1:n habe ich keine probleme. zu der aufgabe a) habe ich folgendes hingeschrieben:
a) bzgl. der Kardinalitätsrelation 1:n ist die Aussag a) sichergestellt, denn zwischen den 3 Entities existieren jeweils 1:1 -Relationen.
so und jetzt müsste ich noch angeben, ob die aussage auch für die min-max notation sichergestellt ist. allerdings kann ich das nicht so ganz deuten, um es erklären zu können.
intuitiv würde ich sagen, dass es bei bei der min-max-notation nicht sichergestellt ist, aber richtig erklären kann ich es nicht.
kann mir jmd. erklären wie das mit der min-max notation zu verstehen ist?
edit: ich hab bissl darüber nachgedacht, und kam zu folgendem schluss:
bzgl. der min-max notation ist die aussage a) nicht sichergestellt, denn betrachtet man nur die Preisträger-Kategorie-Beziehung, so besagt diese: "Einem Preisträger kann in minimal einer und maximal in mehreren Kategorien ein Preis verliehen werden. Allerdings kann es in einer kategorie minimal keinen und maximal mehrere Preisträger geben."
und dass es eben mehrere Preisträger geben kann, ist ein widerspruch zu der aussage a)
die aufgabe b) bearbeite ich noch.
bei der Kardinalitätsrelation 1:n habe ich keine probleme. zu der aufgabe a) habe ich folgendes hingeschrieben:
a) bzgl. der Kardinalitätsrelation 1:n ist die Aussag a) sichergestellt, denn zwischen den 3 Entities existieren jeweils 1:1 -Relationen.
so und jetzt müsste ich noch angeben, ob die aussage auch für die min-max notation sichergestellt ist. allerdings kann ich das nicht so ganz deuten, um es erklären zu können.
intuitiv würde ich sagen, dass es bei bei der min-max-notation nicht sichergestellt ist, aber richtig erklären kann ich es nicht.
kann mir jmd. erklären wie das mit der min-max notation zu verstehen ist?
edit: ich hab bissl darüber nachgedacht, und kam zu folgendem schluss:
bzgl. der min-max notation ist die aussage a) nicht sichergestellt, denn betrachtet man nur die Preisträger-Kategorie-Beziehung, so besagt diese: "Einem Preisträger kann in minimal einer und maximal in mehreren Kategorien ein Preis verliehen werden. Allerdings kann es in einer kategorie minimal keinen und maximal mehrere Preisträger geben."
und dass es eben mehrere Preisträger geben kann, ist ein widerspruch zu der aussage a)
die aufgabe b) bearbeite ich noch.